Important
La traduction est le fruit d’un effort communautaire auquel vous pouvez vous joindre. Cette page est actuellement traduite à 98.39%.
7. Topologie
Objectifs : |
Comprendre la topologie des données vecteur |
|
Mots clés : |
Vecteur, topologie, règles de topologie, erreurs topologiques, rayon de recherches, distance d’accrochage, entité simple |
7.1. Aperçu
La topologie exprime les relations spatiales entre des entités vectorielles (points, polylignes, polygones) connectées ou adjacentes dans un SIG. Des données topologiques ou basées sur une topologie sont utiles pour détecter et corriger les erreurs de numérisation (par ex. deux lignes sur une couche vectorielle de routes qui ne se croisent pas parfaitement à une intersection). La topologie est nécessaire pour effectuer certains types d’analyse spatiale, comme l’analyse de réseau.
Imaginez que vous vous rendiez à Londres. Au cours d’un circuit touristique, vous prévoyez de visiter d’abord la cathédrale Saint-Paul et, dans l’après-midi, le marché de Covent Garden pour acheter des souvenirs. En regardant le plan du métro de Londres (voir Fig. 7.2), vous devez trouver des trains de correspondance pour vous rendre de Covent Garden à St Paul. Cela nécessite des informations topologiques (données) sur les endroits où il est possible de changer de train. En regardant une carte du métro, les relations topologiques sont illustrées par des cercles qui montrent la connectivité.
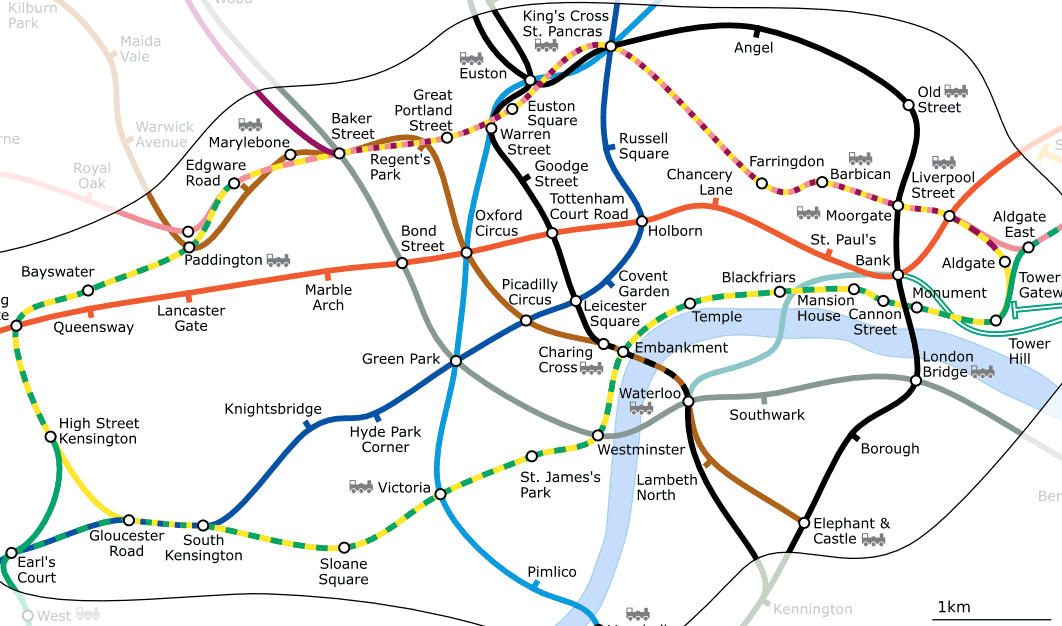
Fig. 7.2 Topologie du réseau de métro de Londres
7.2. Erreurs topologiques
Il existe différents types d’erreurs topologiques, qui peuvent être regroupés selon que les entités vecteur sont des polygones ou des polylignes. Les erreurs topologiques avec les éléments polygones peuvent inclure des polygones non fermés, des espaces entre les bords des polygones ou des bords de polygones qui se chevauchent. Une erreur topologique courante avec les entités polylignes est qu’elles ne se rejoignent pas parfaitement en un point (nœud). Ce type d’erreur est appelé undershoot si un espace existe entre les lignes, et overshoot si une ligne se termine au-delà de la ligne à laquelle elle devrait se connecter (voir Fig. 7.3).
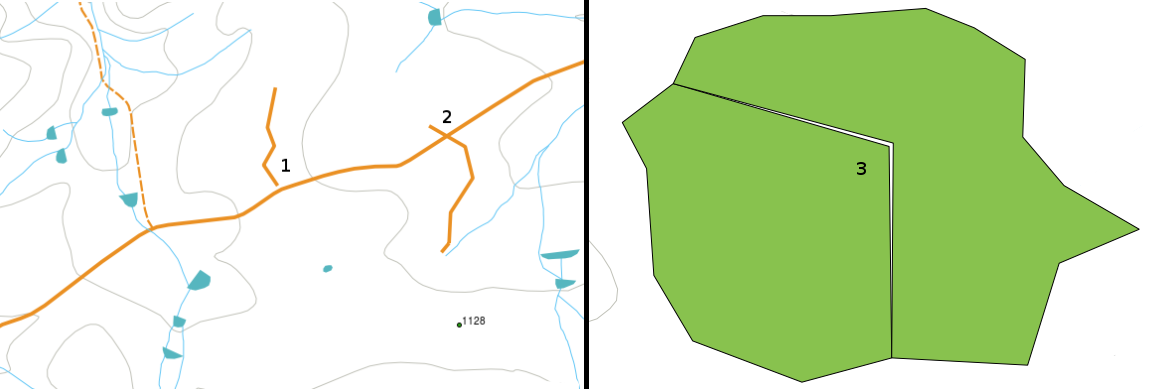
Fig. 7.3 Des dépassements négatifs (1) se produisent lorsque des lignes vectorielles numérisées qui doivent se connecter les unes aux autres ne se touchent pas. Des dépassements (2) arrivent si une ligne se termine au-delà de la ligne avec laquelle elle doit être connectée. Des éclats (3) se produisent lorsque les sommets de deux polygones ne correspondent pas à leurs bordures.
Le résultat des erreurs de dépassement et de dépassement négatif à la fin des lignes sont appelées “nœuds pendants”. Les nœuds pendants sont acceptables dans certains cas, par exemple s’ils sont attachés à des impasses.
Les erreurs topologiques brisent la relation entre les entités. Ces erreurs doivent être fixées afin de pouvoir analyser les données vectorielles avec des procédures telles que l’analyse de réseau (par ex. trouver le meilleur itinéraire à travers un réseau de routes) ou les mesures (par ex. trouver la longueur d’une rivière). En plus de la topologie et étant utile pour l’analyse des réseaux et les mesures, il y a d’autres raisons pour lesquelles il est important et utile de créer ou d’avoir des données vectorielles avec une topologie correcte. Imaginez simplement que vous numérisez une carte de limites municipales pour votre province et les polygones se superposent ou présentent des éclats. Si de telles erreurs étaient présentes, vous seriez en mesure d’utiliser les outils de mesure, mais les résultats que vous obtenez seraient incorrects. Vous ne connaîtrez pas la zone correcte pour n’importe quelle municipalité et vous ne serez pas capable de définir exactement où sont les limites entres les municipalités.
Ce n’est pas seulement important pour votre propre analyse de créer et d’avoir des données topologiquement correctes, mais également pour les personnes à qui vous transmettez les données. Ils attendent que vos données et les résultats d’analyse soient corrects !
7.3. Règles topologiques
Heureusement, beaucoup d’erreurs courantes pouvant survenir lors de la numérisation des entités vectorielles peuvent être prévenues avec des règles topologiques qui sont mises en œuvre dans de nombreuses applications SIG.
Excepté pour certains formats spéciaux de données SIG, la topologie n’est généralement pas appliquée par défaut. Beaucoup de SIG courants, comme QGIS, définissent la topologie comme des règles de relations et laissent l’utilisateur choisir les règles, et le cas échéant les implémenter dans une couche vectorielle.
La liste suivante montre quelques exemples de cas dans lesquels des règles topologiques peuvent être définies pour de véritables entités du monde dans une carte vectorielle :
Les bords de la région d’une carte de municipalité ne doivent pas se chevaucher.
Les bords de la région d’une carte de municipalité ne doivent pas avoir d’espaces (éclats).
Les polygones montrant les limites de propriété doivent être fermés. Les dépassements négatifs et les dépassements des lignes de limites ne sont pas autorisés.
Les lignes de contour dans une couche vectorielle ne doivent pas se croiser (s’entrecouper l’une l’autre).
7.4. Outils topologiques
De nombreuses applications SIG fournissent des outils d’édition topologique. Par exemple, dans QGIS, vous pouvez activer l’édition topologique pour améliorer l’édition et le maintien des limites communes dans les couches de polygones. Un SIG tel que QGIS “détecte” une frontière partagée dans une carte polygonale. Il vous suffit donc de déplacer le sommet d’un polygone pour que QGIS assure la mise à jour des autres polygones, comme le montre Fig. 7.4 (1).
Une autre option topologique vous permet d’empêcher les chevauchements de polygones pendant la numérisation (voir Fig. 7.4 (2)). Si vous avez déjà un polygone, il est possible avec cette option de numériser un second polygone adjacent de sorte que les deux polygones se chevauchent et que QGIS clive ensuite le second polygone sur la limite commune.
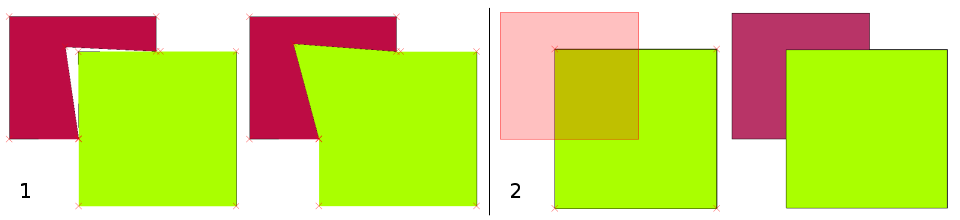
Fig. 7.4 (1) Topological editing to detect shared boundaries, when moving vertices. When moving a vertex, all features that share that vertex are updated. (2) To avoid polygon overlaps, when a new polygon is digitised (shown in red) it is clipped to avoid overlapping neighbouring areas.
7.5. Distance d’accrochage
La distance d’accrochage est la distance utilisée par un SIG pour rechercher le sommet et/ou le segment le plus proche que vous essayez de connecter lorsque vous numérisez. Un segment est une ligne droite formée entre deux sommets dans une géométrie de polygone ou de polyligne. Si vous n’êtes pas à l’intérieur de la distance d’accrochage, un SIG tel que QGIS laissera le sommet là où vous relâchez le bouton de la souris, au lieu de l’accrocher à un sommet et/ou un segment existant (voir Fig. 7.5).
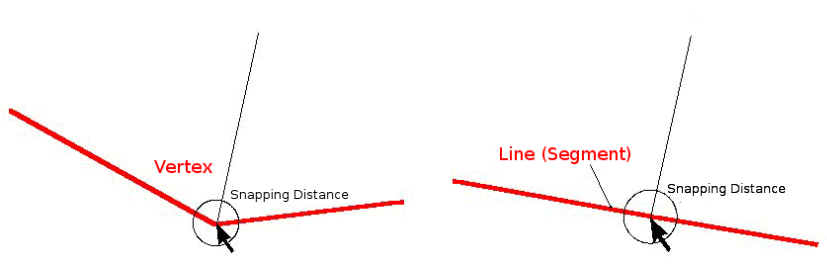
Fig. 7.5 La distance d’accrochage (cercle noir) est définie dans les unités de carte (par ex. degrés décimaux) pour s’accrocher soit aux sommets soit aux segments.
7.6. Rayon de recherche
Le rayon de recherche est la distance qu’un SIG utilise pour chercher le sommet le plus proche vers lequel vous essayez de bouger lorsque vous cliquez sur la carte. Si vous n’êtes pas dans le rayon de recherche, le SIG ne trouvera et ne sélectionnera pas de sommet ou d’entité pour la numérisation. En principe, le rayon de recherche est presque similaire à la fonctionnalité de la distance d’accrochage.
La distance d’accrochage et le rayon de recherche sont tous les deux exprimés en unités de la carte donc vous devrez expérimenter pour trouver la valeur qui vous convient. Si vous indiquez une valeur trop grosse, le SIG peut s’accrocher sur un mauvais sommet, spécialement si vous travaillez avec un grand nombre de sommets proches les uns des autres. Si vous indiquez un rayon de recherche trop petit, l’application SIG ne pourra pas trouver d’entité ou de sommet à modifier ou à éditer.
7.7. Problèmes courants / Choses à savoir
Principalement conçues pour la simplicité et pour un rendu rapide, mais pas pour l’analyse de données qui nécessite une topologie (comme la recherche de routes à travers un réseau), de nombreuses applications SIG sont capables d’afficher des données topologiques et des fonctionnalités simples ensemble et certaines peuvent également créer, modifier et analyser les deux.
7.8. Qu’avons-nous appris?
Faisons le point sur ce que nous avons abordé dans cette partie :
La Topologie montrent les relations de voisinage entre les entités vecteurs.
La topologie en SIG est accessible via des outils topologiques.
La topologie peut être utilisée pour détecter et corriger les erreurs de numérisation.
Pour certains outils, comme l”analyse de réseaux, des données topologiques sont essentielles.
La distance d’accrochage et le rayon de recherche nous aide à numériser des données vectorielles topologiquement correctes.
Les données Entités simples ne constituent pas un format de données topologiquement correct mais il est couramment utilisé par les applications de SIG.
7.9. Maintenant, essayez !
Voici quelques pistes d’actions à essayer avec vos élèves :
Marquez les arrêts de votre bus local sur une carte topographique et demandez ensuite à vos élèves de trouver la route la plus courte entre deux arrêts.
Pensez à comment vous pourriez créer des entités vectorielles dans un SIG pour représenter un réseau de routes topologique de votre ville. Quelles règles topologiques sont importantes et quels outils vos enseignants utilisent-ils dans QGIS pour être certains que la nouvelle couche de route est topologiquement correcte ?
7.10. Pour aller un peu plus loin…
Si vous n’avez pas d’ordinateur à disposition, vous pouvez utiliser une carte du réseau d’un bus ou d’un chemin de fer et discuter des relations spatiales et de la topologie avec vos enseignants.
7.11. Pour aller plus loin
Livres :
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Sites Web :
Le Guide Utilisateur de QGIS apporte de plus amples informations sur l’édition topologique au sein de QGIS.
7.12. La suite ?
Dans la section qui suit, nous regarderons de plus près les Systèmes de Coordonnées de Référence pour comprendre comment nous rapportons les données de notre terre sphérique sur des cartes plates !
